Вопрос 40: Гравитационный поиск.

Источники: билеты по ОИИ

В этом вопросе нижние индексы обозначаются через нижнее подчёркивание, потому что по-другому очень долго, верхние - через степень. Пример: m i-тое это: m_i, m с верхним индексом i это m^i

Общее
Алгоритмы, вдохновлённые физическими явлениями, характерны тем, что опираются на законы физики. Примеры алгоритмов: алгоритм имитации отжига, гармонический поиск, алгоритм оптимизации центральной силой.

Гравитационный поиск

Алгоритм гравитационного поиска является развитием детерминированного алгоритма глобального многомерного поиска, получившего название алгоритма оптимизации центральной силой. Алгоритм гравитационного поиска является стохастическим, начальное распределение носит случайный характер; гравитационная постоянная изменяется в процессе поиска по некоторым правилам. Алгоритм использует аналогию движения тяжелых тел вследствие их гравитационного взаимодействия.

На каждой итерции

Алгоритм гравитационного поиска использует следующее правило вычисления силы, действующей на массу m_i со стороны массы m_j по k-му измерению:

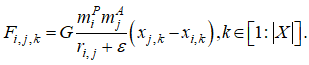
Здесь eps - малая константа, r_i,j - текущее евклидово расстояние между массами m_i и m_j. Гравитационную постоянную G уменьшаем с ростом числа итераций по правилу:

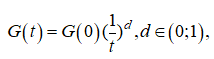
где G(0) – её начальное значение, а d - свободный параметр алгоритма. Суммарную силу F_i,j,k действующую на зонд s_i по k-му измерению, полагают случайной величиной, равной

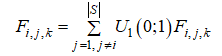
Ускорение указанного зонда по тому же измерению находим по формуле

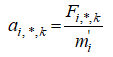
Если положение зонда s_i по k-му измерению на данной итерации есть x_i,k , то на следующей итерации его определяет выражение

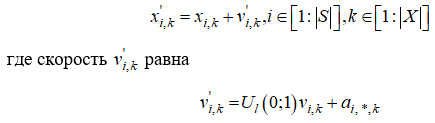
Простейший алгоритм гравитационного поиска предполагает равенство активной, пассивной и инертной масс m^A, m^P, m^l точнее говоря, полагается, что

(я считпю, что это критерий останова)

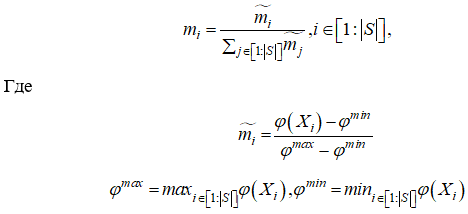
Эффективность поиска с помощью алгоритма гравитационного поиска может быть повышена, если с ростом числа итераций сокращать по некоторому правилу в формуле число зондов, оставляя лишь наиболее массивные из них. Тем самым можно обеспечить лучший компромисс между диверсификацией поиска на начальных итерациях и его интенсификацией на завершающих итерациях. Обозначим S'' текущий набор лучших (самых тяжелых) зондов, а I'' - совокупность номеров этих зондов. Тогда модифицированная формула примет вид

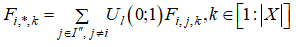
Число |S’’| лучших зондов с ростом числа итераций уменьшают, например, по линеqному закону, так что, в конце концов, остается лишь один зонд, притягивающий остальные зонды.