Вопрос 41: Электромагнитный поиск.

(В этом вопросе нижние индексы обозначаются через нижнее подчёркивание, потому что по-другому очень долго, верхние - через степень. Пример: m i-тое это: m_i, m с верхним индексом i это m^i)

Общее Алгоритмы, вдохновлённые физическими явлениями, характерны тем, что опираются на законы физики. Примеры алгоритмов: алгоритм имитации отжига, гармонический поиск, алгоритм оптимизации центральной силой.

Электромагнитный поиск

Общая схема алгоритма включает в себя следующие шаги. 1) Инициализируем популяцию. 2) Выполняем локальный поиск. 3) Вычисляем суммарные силы, действующие на каждую из частиц популяции. 4) Реализуем перемещение частиц. 5) Выполняем проверку выполнения условия окончания итераций и в зависимости от итогов этой проверки либо завершаем вычисления, либо переходим к шагу 2.

Об этапах

Инициализация популяции включает в себя: -генерацию |S| точек, равномерно распределенных в гиперпараллелепипеде П

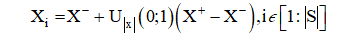
-Во-вторых, на данном этапе производим вычисление исходных значений фитнес-функции 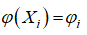и определяем лучшее из этих значений

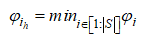
Локальный поиск выполняем для каждого из текущих положений частиц X_i с целью сбора локальной информации о ее окружении. Этот поиск может быть реализован с помощью любого из детерминированных или стохастических алгоритмов локальной оптимизации. Авторы алгоритма предлагают использовать линейный стохастический поиск.

Вычисление суммарных сил

На текущей итерации заряду частицы s_i ставим в соответствие величину

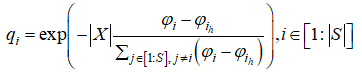
которая представляет собой нормированное значение фитнес-функции в текущем положении X_i этой частицы. Здесь 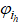- минимальное достигнутое популяцией к данной итерации значение этой функции. Множитель |Х| добавлен с целью предотвращения слишком малых абсолютных значений величины под знаком экспоненциальной функции при высоких размерностях поискового пространства. Аргумент этой функции во всех случаях неположителен, так что заряд всегда положителен и принадлежит интервалу (0; 1].

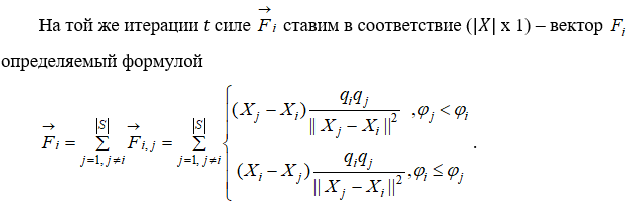
Из формулы выше следует, что частица с лучшим значением исследуемой функции притягивает частицу с худшими значениями этой функции, и наоборот - вторая частица отталкивает первую. Из этой же формулы вытекает, что частица,имеющая на данной итерации значение фитнес-функции, равное 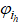, притягивает все остальные частицы популяции.

Перемещение частиц выполняем по правилу

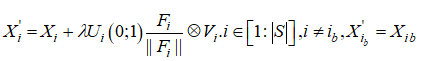
здесь лямбда - шаг перемещения (свободный параметр); компоненты вектора V_i имеют значения

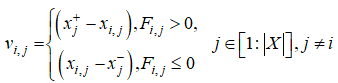
Формулы выше означают, что при перемещении частицы из положения X_i в положение X'_i используем нормированную силу. По каждому из измерений вектора Х перемещение производим с шагом случайного размера в направлении соответствующей верхней или нижней границ параллелепипеда П. Частицу s_ib на данной итерации не перемещаем. Окончание итераций В оригинальной версии алгоритма условием завершения вычислений является достижение заданного числа итераций i. Авторы алгоритма рекомендуют использовать следующие значения свободных параметров:

• число итераций локального поиска t в несколько раз превышает величину |X|;
• величина, определяющая максимально допустимую величину шага локального поиска, принимает значения от 10^(-2) до 10^(-4);
• максимальное число итераций t = 25|X|. Авторы алгоритма выполнили широкое экспериментальное сравнение его эффективности с эффективностью многих известных популяционных и непопуляционных алгоритмов глобальной оптимизации. Исследование показывает, что обычно алгоритм ЕМ показывает сравнимые, а часто лучшие результаты, чем другие алгоритмы.