Вопрос 12: Многокритериальная оптимизация. Понятие множества Парето, доминируемых и недоминируемых решений. Фронт Парето.

Многокритериальная оптимизация – раздел теории оптимизации, рассматривающий задачи, в которых целевая функция – векторная величина. Эти задачи широко распространены во всех инженерных областях.

Многокритериальные задачи обычно не имеют однозначного решения в терминах классической теории оптимизации, так как глобальные минимумы различных компонентов векторной целевой функции не совпадают. В этом случае часто ставится задача найти не одно решение, а набор решений, определяющих наилучший компромисс между целевыми функциями. Задача многокритериальной оптимизации может быть записана в виде:

$\lbrack \vec{x^{*}} \rbrack = \text{argmin}\vec{f}(\vec{x})$

Введем понятие доминируемого и недоминируемого решений. Решение $x_1$ доминирует над решением $x_2$, т.е. $x_1 \prec x_2$, если $f_i(x_1) \leq f_i(x_2) \forall i$. Недоминируемое решение $x_{ND}$ - такое, что любой из компонентов целевой функции

$f_i(x_{ND})\leq f_i(x^{*}) \forall x^{*}$

где $x$ - одно из решений.

Один из способов решения задачи многокритериальной оптимизации – нахождение решения в виде множества Парето. Множество Парето $P$ - это набор недоминируемых решений. Образ множества Парето в пространстве значений целевых функций называется фронтом Парето ${F} = {y = f(x); x \in P}$

(Определение из алгебры: Пусть задано отображение $f:E \to F$ и множество $D \subset E$. Множество элементов из $F$, каждый из которых является образом хотя бы одного элемента из D при отображении f, называется образом множества D и обозначается $f(D)$. Т.е. Образ множества - это множество элементов, которые являются образами других элементов при отображении.)

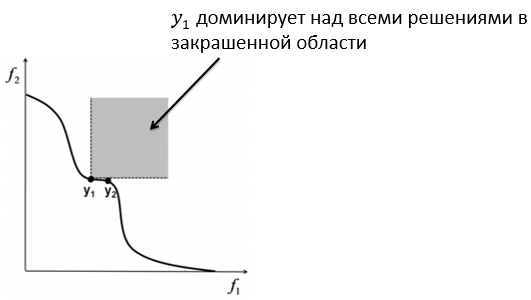
Графическим изображением множества Парето, или множества недомирируемых решений, является фронт Парето. Пусть многокритериальная оптимизация производится по двум функциям $f_1$ и $f_2$. Тогда линия, соответствующая всем недомирируемым решениям, будет являться фронтом Парето.