Вопрос 15: Метод Хука-Дживса.

Зависимые вопросы

• Онлайн решение методом Хукка-Дживса
• Практика

Определение

Метод Хука — Дживса служит для поиска безусловного локального экстремума функции и относится к прямым методам, то есть опирается непосредственно на значения функции. Алгоритм делится на две фазы: исследующий поиск и поиск по образцу.

Подготовка

Необходимо задать стартовую точку, начальный шаг, точность, параметр для шага по образцу:

• $\overline{x}_{1}$ = ($x_1$; $x_2$) = [3; 1];
• h = 1. Можно взять разные шаги для каждой из осей - это одна из модификаций алгоритма;
• T = 0.5;
• $\lambda$ = 2.

Исследующий поиск

Вычисляем значения функции в точках $x_1 + h$ и $x_1 - h$ (где $x_1$ — первая координата точки, а $h$ — соответственно значение шага по этой координате) и переходим в точку с наименьшим значением функции. В этой точке замораживаем значения всех координат кроме 2-й, вычисляем значения функции в точках $x_2 + h$ и $x_2 - h$, переходим в точку с наименьшим значением функции и т. д. для всех координат. В случае, если для какой-нибудь координаты значение в исходной точке меньше, чем значения для обоих направлений шага, то шаг по этой координате уменьшается. Когда шаги по всем координатам $h$ станут меньше соответствующих значений T, алгоритм завершается, и точка $\overline{x_1}$ признаётся точкой минимума. Иллюстрация исследующего поиска:

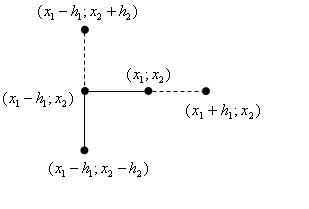
Поиск по образцу

На этапе поиска по образцу откладывается точка 3 в направлении от 1 к 2 на том же расстоянии. Её координаты получаются по формуле ${\displaystyle {\overline {x}}_{3}={\overline {x}}_{1}+\lambda ({\overline {x}}_{2}-{\overline {x}}_{1})}$, где $x_i$ — точка с номером i, λ — параметр алгоритм. Затем в новой точке 3 проводится исследующий поиск, как на 1 фазе алгоритма, за исключением того, что шаг на этой фазе не уменьшается. Если на этой фазе в результате исследующего поиска удалось получить точку 4, отличную от точки 3, то точку 2 переобозначим на 1, а 4 на 2 и повторим поиск по образцу. В случае если не удаётся найти точку 4, отличную от точки 3, то точку 2 переобозначим на точку 1 и повторим 1-ю фазу алгоритма — исследующий поиск. Иллюстрация: