Вопрос 13: Многокритериальная оптимизация. Метод взвешенной суммы. Метод взвешенной метрики. Генетические алгоритмы.

Зависимые вопросы

• Вопрос 12: Многокритериальная оптимизация. Понятие множества Парето, доминируемых и недоминируемых решений. Фронт Парето.
• Вопрос 5: Генетический алгоритм. Определение. Общая схема. Понятие хромосомы, гена, отбора.
• Вопрос 6: Виды кроссовера в генетическом алгоритме.
• Вопрос 8: Бинарное и вещественное кодирование в генетическом алгоритме. Код Грея.
• Вопрос 9: Понятие элитизма. Алгоритм островов. Клеточный ГА.

Для получения оптимальных по Парето решений часто используют методы скаляризации. Поскольку целевая функция задачи многокритериальной оптимизации имеет векторные значения, ее превращают в функцию со скалярным значением. Таким образом, задача многокритериальной оптимизации сводится к задаче оптимизации с одной скалярной целевой функцией. Функция скаляризации должна удовлетворять следующим условиям.

Пусть $F$ - функция скаляризации, которая превращает векторную функцию $\vec{y} = \vec{f}(\vec{x})$ в скалярную. Если $F$ сохраняет упорядоченность по Парето, то есть, если для произвольных $\vec{y^{1}}, \vec{y^{2}} \in \vec{f}(X)$ выполняется:

$\vec{y^{1}} \leq \vec{y^{2}} \Rightarrow F(\vec{y^{1}}) < F(\vec{y^{2}})$,

тогда решение, что минимизирует $F$ на $X$ является решением по Парето. Если же

$\vec{y^{1}} < \vec{y^{2}} \Rightarrow F(\vec{y^{1}}) < F(\vec{y^{2}})$,

тогда решение, что минимизирует $F$ на $X$ является слабым по Парето. Если $F$ непрерывна и $\vec{x^{0}}$ единственная точка минимума $F$ на $X$, тогда $\vec{x^{0}}$ является решением по Парето.

Метод взвешенной суммы

Это один из методов скаляризации. Суть метода:

Целевая функция скаляризуется путем назначения весовых коэффициентов значения $w_m$ каждому из компонент решения $f_m$.

$F(x) = \sum_{ m = 1}^{M}w_mf_m(x)$

Достоинство метода заключается в его простоте. Недостатки:

• Нужна настройка весов;
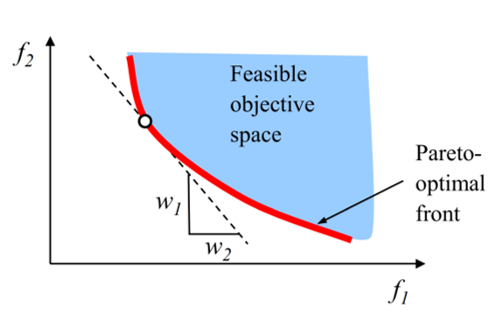
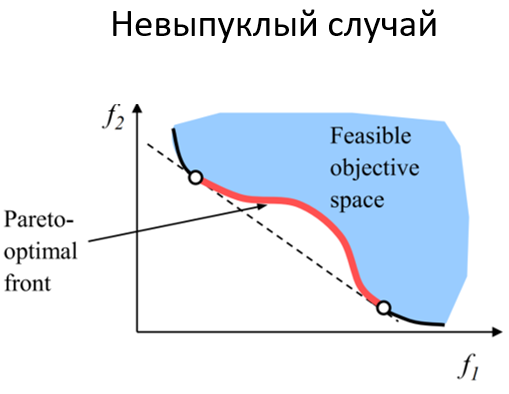
• Нельзя найти оптимальное по Парето решение, если пространство целевой функции не выпуклое. Выпуклый и невыпуклый случаи проиллюстрированы на картинках ниже.

Метод взвешенной метрики

Ещё один способ скаляризации функции. Суть метода заключется в сужения интервалов весов критериев. Метрика характеризует расстояние между двумя точками в многомерном пространстве.

Целевая функция представляется в виде комбинации взвешенных расстояний до некоторого идеального решения $z^{*}$. Расстояние измеряется по метрике Чебышева в $m$-мерном критериальном пространстве (в формуле ниже $w_m$ - весовой коэффициент, остальное - Чебышевская метрика.)

$l_p(x) = (\sum_{m = 1}^{M}w_m{|f_m(x) - {z_m}^{*}}|^p)^{1/p}$

(Определение, которое не пригодится, Артур об этом не говорил, но на всякий случай: метрика Чебышева - это частный случай $L_p$ метрик. $L_p$ метрика - это метрика в пространстве $L_p$.$L_p$ пространство - это пространства измеримых функций, таких, что их $p$-я степень интегрируема, где $p \geq 1$.)

На картинках ниже $z^{*}$ - идеальное решение, а $a$, $b$ - это какие-то решения $f_m(x)$.

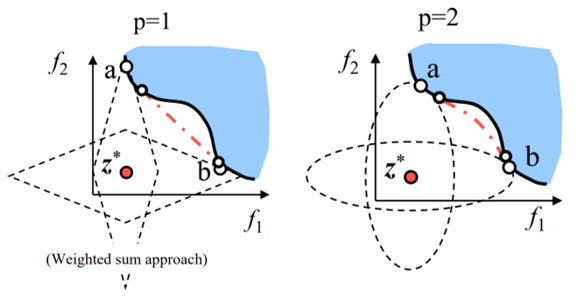
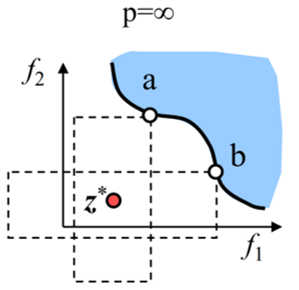
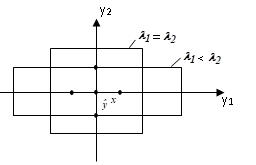
Картинки выше представлены для равных весов. При неравных значениях линии вытягиваются в направлении наименьших весов (картинка ниже, там лямбда - это весы).

Достоинство: Метод по метрике Чебышева гарантирует нахождение всех Парето-оптимальных решений вблизи $z^{*}$.

Недостатки:

• Нужно априори знать $z^{*}$
• Нужно знать границы значений ЦФ
• При больших p задача становится недифференцируемой

Генетические алгоритмы

В то время как традиционные алгоритмы оперируют с одним из возможных решений, генетический алгоритм оперует с множеством решений, что является преимуществом в рамках многокритериальной оптимизации. Алгоритмы описанные ниже предназначаются для определения того, какие из решений доминируют.

1. Метод Кунга

Ш1. Отсортируем популяцию в порядке убывания важности первой целевой функции и назовём популяцию $P$.

Ш2. Вызвать рекурсивную функцию Front(P).

Суть функции: отсортировать в зависимости от того, является ли решение доминантным.

Иллюстрация работы алгоритма:

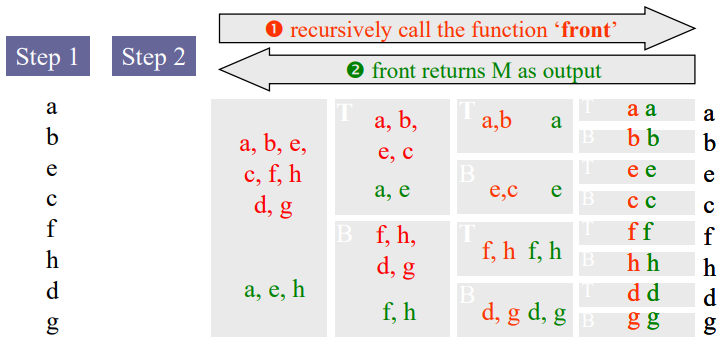
Пример результата работы алгоритма:

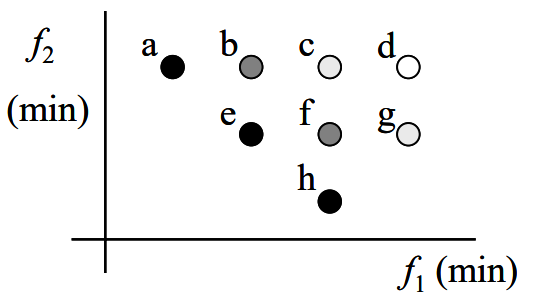
Достоинство: высокая эффективность.

2. Элитарная недоминируемая сортировка

Определение. Ранг k особи соответствует числу особей в текущей популяции, над которыми она доминирует.

Общая схема алгоритма:

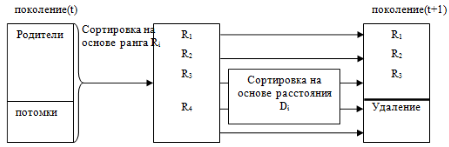
Ш1.Объединяем решения в несколько взаимоисключающих множеств путём сортировки по значению ранга.

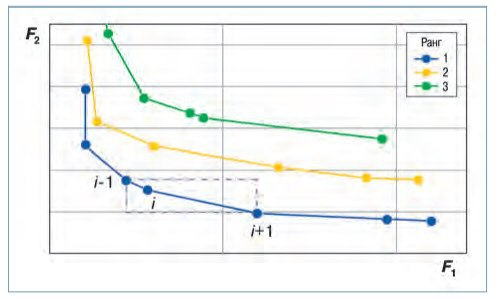
Ш2.Определение расстояния кроудинга

Сортируются элементы внутри каждого ранга.

Для каждого элемента расчитывается расстояние кроудинга по формуле:

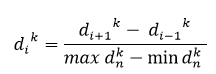
где $k$ - это ранг, $n$ - количество особей одного ранга.

Расстояние кроудинга для i-й особи равно нормированной сумме сторон прямоугольника, вершинами которого являются особи i – 1 и i + 1. Чем больше расстояние кроудинга, тем равномернее распределение особей на фронте.

Ш3.На основе значений ранга и расстояния Кроудинга производится турнирный отбор.

Решение $i$ побеждает решение j, если:

• Решение i имеет лучший ранг;
• При равном ранге групповая дистанция i меньше.

Достоинства алгоритма:

• Многообразие в популяции не нужно искусственно поддерживать благодаря групповому отбору;
• Элитизм защищает найденные лучшие решения от исчезновения.

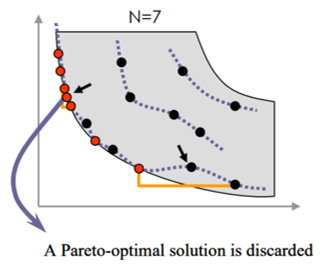
Недостаток:

Число оптимальных решений на фронте Парето фиксированное, некоторые решения могут потеряться.