Вопрос 14: Метод симплексов

Метод безусловной оптимизации функции от нескольких переменных, не использующий градиентов функции. Суть метода заключается в последовательном перемещении и деформировании симплекса вокруг точки экстремума.

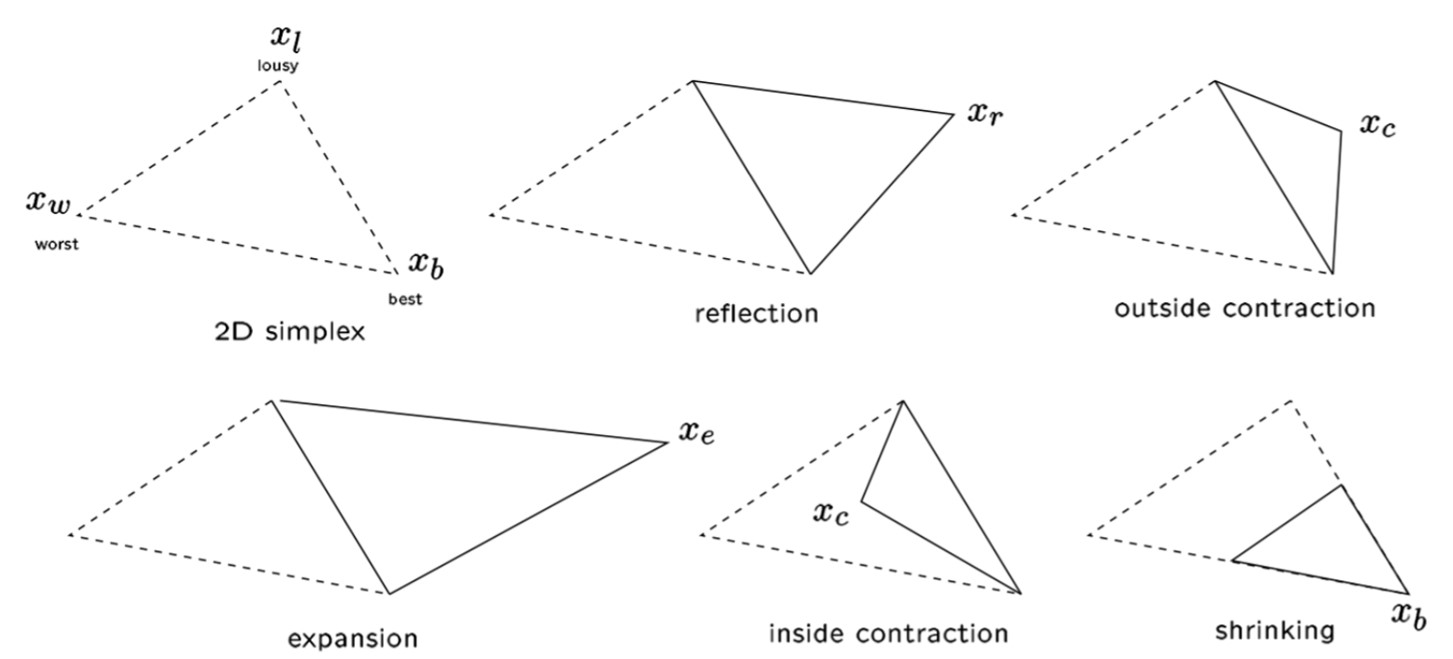
Симплекс – n-мерное обобщение треугольника:

Операции над симплексами

Алгоритм

Параметры метода: коэффициент отражения $\alpha$ > 0, обычно выбирается равным 1. коэффициент сжатия $\beta$ > 0, обычно выбирается равным 0,5. коэффициент растяжения $\gamma$ > 0, обычно выбирается равным 2.

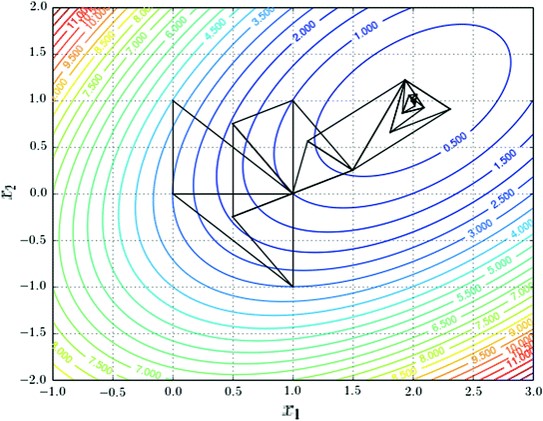
Пусть требуется найти безусловный минимум функции 2 переменных. Тогда симплекс будет иметь размерность равную 3.

Шаг 1 - обозначение точек

Выберем три точки – вершины треугольника. Вычислим значения целевой функции в вершинах и обозначим их как best, lousy и worst: $f_b$, $f_l$, $f_w$. Соответствующие точки пространства обозначим как $x_b, x_l, x_w$.

Шаг 2 - отражение

Найдем среднее арифметическое всех точек симплекса, кроме худшей $x_w$: $x_a=\frac{1}{n}\sum_{i=0,i\neq w}^{n+1}x_i$ Для нашего случая формула будет выглядеть следующим образом: $x_a = (\frac{x_l+x_b}{2}; \frac{y_l+y_b}{2})$ Найдем отражение худшей точки и вычислим значение функции в этой точке $f_r = f(x_r)$: $x_r = x_a + \alpha(x_a-x_w)$

Шаг 3 - смотрим какое место между всеми точками заняла отраженная точка

Если $f_r < f_b$, то направление удачное и можно увеличить шаг: найдем "растяжение" и вычислим значение функции в этой точке $f_e=f(x_e)$: $x_e=x_r+\gamma(x_r-x_a)$

Если $f_e<f_r$, то $x_w = x_e$ и переходим на Шаг 6. Если $f_r<f_e$, то $x_w = x_r$ и переходим на Шаг 6. Если $f_r < f_l$, то $x_w = x_r$ и переходим на Шаг 6. Если $f_r > f_w$, то на Шаг 4. Если $f_r < f_w$, то на Шаг 5.

Шаг 4 - внутреннее сжатие

Используя среднюю точку $x_a$ и худшую точку $x_w$, найдем $x_c$ и значение функции в этой точке $f_c = f(x_c)$: $x_c = x_a - \beta(x_a-x_w)$ Если $f_c < f_w$, то $x_w = x_c$ и переходим к Шагу 6. Иначе проводим "сокращение" - обновляем все вершины, кроме лучшей по следующему соотношению: $x_i = x_b + \rho(x_i-x_b)$ и переходим к Шагу 6.

Шаг 5 - внешнее сжатие

Используя среднюю точку $x_a$ и худшую точку $x_w$, найдем $x_o$ и значение функции в этой точке $f_o = f(x_o)$: $x_o = x_a + \beta(x_a-x_w)$ Если $f_o < f_r$, то $x_w = x_o$ и переходим к Шагу 6. Иначе проводим "сокращение" - обновляем все вершины, кроме лучшей по следующему соотношению:
$x_i = x_b + \rho(x_i-x_b)$ и переходим к Шагу 6.

Шаг 6 - проверка сходимости

Если алгоритм сходится или достигнут критерий остановки, заканчиваем работу. Иначе проводим переоценку точек: находим значения функций в этих точках и обозначаем их как best, lousy и worst ($x_b, x_l, x_w$) и переходим к Шагу 2.

Пример выполнения метода